Arranging Mega Man tiles with Block-Swapping MCMC
Discrete Markov Random Fields, or Undirected Graphical Models, can be sampled from using Gibbs Sampling and approximately optimized with Simulated Annealing (a family of algorithms which often employ Gibbs Sampling). Gibbs sampling unfortunately lacks the ability to deal with one-of-each constraints over the graph. In this post, I show how it is possible to enforce the one-of-each constraint by swapping variables (rather than resampling them conditioned under a Markov blanket). This can be applied to optimizing tileset palette arrangements.
Motivation
Many video game levels are built by assembling a limited set of square tiles, such as this level from Mega Man 3 (1990):

(Credit to VGMaps Atlas user Revned)
When analyzing these tilesets or when using them to construct new levels (e.g. for a ROMHack), it is a trivial task to write a program to identify what tiles are in the level. However, the raw tile palette will look scrambled and hard to understand. For example, consider the following machine-ripped palette of a stage from Mega Man 9 (2008):

(Ripped from a map by VGMaps Atlas user Revned)
However, arranging the tile palette into something usable or easy to understand is an arduous task typically done by hand. It’s important to have a well-arranged tileset if one wants to use it in a ROMHack to create new levels. Arranging the tiles considerably improves readability, but this tileset took me more than an hour to arrange into something usable:

An automated solution is needed. To do this, we first need to decide upon a metric by which to score a proposed arrangement.
Defining a Scoring Rubric
Markov chains can produce amusing epigraphs by reading a body of source text and then constructing a sentence by randomly generating words weighted according to how frequently they are found next to each other. One also use Markov chains to score two sentences according to how likely they are. For example, the sentence
The Quick Brown Fox Jumped over the Lazy Dog
Might be considerably more likely than
Brown The Quick Jumped Fox the Dog Lazy over
The same principles that generate almost-coherent sentences can be extended from a one-dimensional directed network like a sentence (in which each node is a word in a linear chain) to an undirected two-dimensional grid (such as a video game map or an image). If we learn an undirected graphical model by observing what tiles frequently appear next to one another (and in which orientations), then it becomes possible to automatically discern that some arrangements of tiles are likely and some are unlikely:
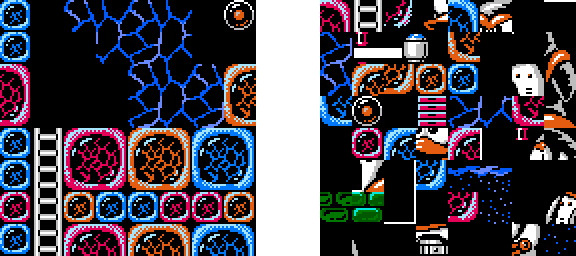
On the left: a likely configuration. On the right: an unlikely configuration.
By defining an “energy function” that we learn from an input game map according to what tiles are next to one another, we can use the same function to state whether an arrangement is “good” (low-energy) or “bad” (high-energy). Because the 2d grid graph neither directed nor a chain, it is not a Markov Chain but rather an Undirected Graphical Model (UGM).
We now have a way to know what arrangements are good and what arrangements are bad – but finding a good arrangement at all turns out to be quite challenging.
Approaches
What doesn’t work
Exact optimization
Initially I tried using an integer linear programming solver to get a globally optimal tile arrangement, but unfortunately the problem was just too hard for it. The Microsoft Z3 SAT solver also was unable to scale beyond extremely tiny palettes.
Gibbs Sampling
Unfortunately, while it is very easy to write a program that samples from a directed Markov chain, it is not easy to sample from an undirected graphical model. One solution is to use Gibbs Sampling. in Gibbs Sampling, we begin with a random arrangement of the tiles and then repeatedly replace tiles with a random tile generated according to the tile’s neighbours. This in theory eventually converges to a region of high probability.
However, if we use this method to generate our palette, we get no guarantee that the end result will contain every tile. So we need to use a slightly different method.
What almost works
Modified Gibbs Sampling via Swapping
The first idea I had to correct Gibbs sampling is to randomly swap tiles instead of resampling tiles in isolation. If we begin with any initialized state that has one of each tile, then this method respects the constraint that there should always be one of each tile. The basic idea is, repeatedly pick a random tile, then consider swapping it with every tile on the board. Randomly pick one of these swaps weighted to how likely the resulting configuration is. This method works moderately well:

Unfortunately, the algorithm gets stuck after a while. In this run, the Penguin enemy aggregates in three different areas, one of which is at the top of the board. At this point, no single swapping of two tiles is favourable, so the algorithm gets stuck in this valley of favourability. The algorithm would have to tile-by-tile move the penguin over from one side of the board to the other, and this is very unlikely. Theoretically, tile swapping is ergodic so it will eventually escape any locally-optimal configuration, but it will take far too long to be useful to us.
The part of the penguin cut off at the top of the board is especially tricky for the algorithm to reconfigure, as that penguin will need to be shifted down in order for the top to meet it. This is due to a lack of periodic boundary conditions. However, implementing periodic boundary conditions will not be very helpful here as (a) the end result does not have periodic boundary conditions (it’s a rectangular image), and (b) it’s still very possible to get stuck even when not near the edge of the board.
What works
Modified Gibbs Sampling via Block-Based Swapping
In order to solve the problem of it being unfavourable to transfer a large block of tiles, we simply allow the algorithm to transfer large blocks of tiles all at once. Instead of picking a random tile to swap at each step, we pick a random rectangle of a random size to swap at each step (including 1x1 rectangles, which are tiles). This is the best result I have been able to produce:
(This is an animated gif; you may need to refresh to see it play.)
Every time I’ve run it on this tileset, the penguin just snaps together in the first thousand iterations (a few seconds in python). This certainly exceeded my expectations!
Block-Based Swapping with Flood-Filled Blocks
The seemingly obvious speedup would be to search for blocks that are highly probable when next to each other (such as bits of a penguin) and preferentially swap those, rather than picking a randomly-sized square with a random location. One way to solidify this notion might be the following method: pick a random tile and grow a rectangle around it so long as, say, the favourability is above-average to do grow it. Surprisingly, while this method does induce many favourable swaps, the data show that it is not very helpful, and possibly detrimental, even when employed in mixture with the previous method.
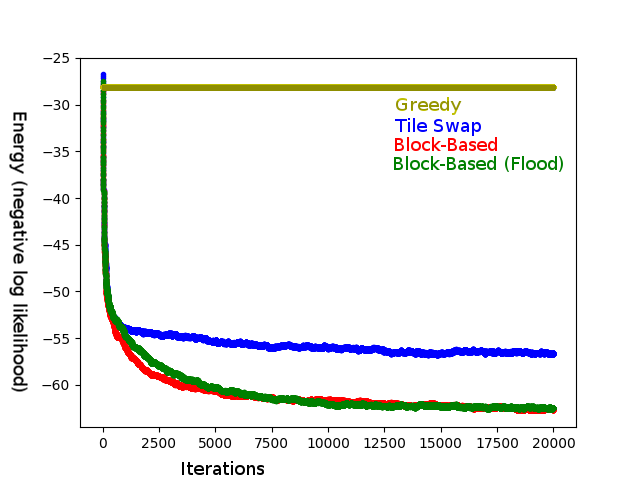
Block-Based and Flood-Fill-Block-Based both stop making significant progress at the same energy, but Block-Based gets there a bit faster. Averaged over 10 trials for each method.
Where to get the algorithm
You can get it on my GitHub repository!